Legalni bukmacherzy > Zastosowanie statystyki w zakładach bukmacherskich

Zastosowanie statystyki w zakładach bukmacherskich

Zastosowanie statystyki w zakładach bukmacherskich

Dla wielu grających matematyka stanowi nieodłączne narzędzie przy podejmowaniu decyzji i określaniu ryzyka dla danego zakładu. Istnieje też rzesza ludzi mających ambiwalentne uczucia względem królowej nauk. Wychodzą oni z założenia, że w sporcie liczą się ludzie a nie liczby.

Nie do końca zgadzam się z tym stwierdzeniem, ponieważ warto by wziąć pod uwagę, że liczby są wymiernym odbiciem formy, możliwości i osiągnięć drużyn lub sportowca. Dlatego analizując dane z przeszłości można określić pewne tendencje, które z dużą dozą prawdopodobieństwa mogą się zdarzyć również i w przyszłości.

Przyszłość jest nieznana, jest to fakt. Jednak historia kołem się toczy i z tym faktem, chcąc, nie chcąc- musimy się zgodzić.

Najczęściej wykorzystywanymi działami matematyki w branży bukmacherskiej (i nie tylko) są statystyka i rachunek prawdopodobieństwa, zresztą obydwie dzieciny są ze sobą bardzo ściśle powiązane.

Z grubsza rzecz biorąc statystyka zajmuje się przede wszystkim analizą danych opisujących jakieś zdarzenie, zjawisko. W przypadku sportu, takimi zdarzeniami są wszelkie policzalne aspekty danej dyscypliny.

Przykładem są nie tylko wyniki spotkań, ale również ilość fauli, rzutów rożnych w piłce nożnej, ilość bloków lub asyst w koszykówce, ilość przebytych z piłką yardów w footballu amerykańskim, czy też suma homerunów w meczu baseballowym. Te wszystkie liczby stanowią dla nas surowy materiał statystyczny, który odpowiednio usystematyzowany i uporządkowany stanie się wartościowym przedmiotem analizy.

W tym artykule chciałbym przedstawić dwa najbardziej użyteczne parametry statystyczne, mianowicie średnią arytmetyczną oraz medianę. Dla wyjaśnienia tylko objaśnię słowo parametr statystyczny – jest nim liczba służąca do syntetycznego opisu struktury zbiorowości. Definicja może brzmi odpychająco, jednak nie jest to nic strasznego.

Parametry dzielą się na cztery grupy: miary położenia, miary zmienności, miary asymetrii oraz miary koncentracji. Ja zajmę się miarami położenia, które z kolei dzielą się na klasyczne oraz pozycyjne.

Do miary klasycznej zalicza się między innymi średnią arytmetyczną (oprócz niej miarami klasycznymi są również średnia harmoniczna oraz geometryczna). Natomiast miary pozycyjne to modalna i kwantyle. Te ostanie dzielą się z kolei na: kwartyle (pierwszy, mediana, trzeci), decyle i centyle.

Spis treści

Średnia arytmetyczna

Pierwszą miarą jaką wezmę „na ruszt” jest średnia arytmetyczna. Z definicji jest to suma wartości cechy mierzalnej dzielona przez liczebność populacji. Wzór średniej arytmetycznej nieważonej zapisany w formie matematycznej wygląda następująco:

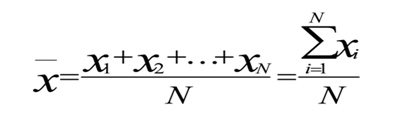
Gdzie:
(x) – oznaczenie średniej arytmetycznej
N – liczba zbiorowości
Xi – wartość zmiennej i-tej jednostki

Mediana

Drugą miarą, którą chciałbym przedstawić jest mediana. Mediana (kwartyl drugi) jest taką wartością cechy w szeregu uporządkowanym, poniżej i powyżej której znajduje się taka sama liczba obserwacji.

Pierwszym krokiem do obliczenia mediany jest uporządkowanie danego szeregu o liczbie „n” obserwacji od najmniejszej do największej. Następnie, jeśli jest to szereg o nieparzystej liczbie obserwacji, miejsce mediany wyznaczamy ze wzoru „n+1/2”. Czyli, gdy szereg składa się z 21 wartości, to wartością mediany będzie: 21+1/2=11 – jedenasta obserwacja w tym szeregu. Gdy liczba obserwacji jest parzysta wyciągamy średnią arytmetyczną ze środkowych obserwacji, czyli wartością n/2 i n/2+1.

Teraz może się to wydawać zagmatwane, dlatego poniżej postaram się to wyjaśnić za pomocą konkretnych przykładów.

Przykłady

Przykład obliczania średniej arytmetycznej i mediany dla szeregu szczegółowego.

Mamy dany ciąg wartości, uporządkowany rosnąco: 0, 1, 1, 1, 1, 1, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 7, 7, 7, 7, 7, 15. liczba obserwacji „n” wynosi 22. A zatem średnia arytmetyczna takiego szeregu będzie wynosiła: (x) = 0+1+1+1+1+1+4+4+4+4+4+5+5+5+5+5+7+7+7+7+7+15/22 = 4,55

Medianę obliczymy następująco: Szereg jest parzysty, a więc korzystamy z drugiego wzoru, stąd:
Me = 1/2 * (Xn/2+Xn/2+1) = 1/2 * (4+5) = 4,5

Jak widać, wyniki nieznacznie się od siebie różnią. Dlaczego zatem stosować dwie różne miary?
Odpowiedź jest prosta.

Średnia arytmetyczna jest bardzo wrażliwa na skrajne wartości szeregów, w przeciwieństwie do mediany, stąd widoczna jest mała rozbieżność w wartościach obu miar.

Mediana dzieli zbiorowość na dwie równe części, skrajne wartości są jakby ucinane. Natomiast średnia nie pomija żadnej wartości, stąd jej wielkość często jest zawyżona lub zaniżona względem rzeczywistych pomiarów.

Najlepszym przykładem będzie choćby średnia zarobków przeciętnego polaka. Sądzę, że gdyby mierzono medianę a nie średnią, wynik ten byłby całkiem inny i na pewno niemal idealnie obrazowałby sytuację w kraju pod tym względem.

Kiedy chcemy wyliczyć średnie wartości w sporcie warto z wrzucić dane do Excela, lub innego arkusza kalkulacyjnego i śmiało zacząć stosować oprócz średniej, również medianę.

Przykład San Antonio Spurs

Dobrym przykładem jest sytuacja San Antonio Spurs. Akurat w przypadku tej drużyny średnia i mediana pokazują dosyć wyraźnie swoje zastosowanie.

I tak dziesięć ostatnich wartości liczb zdobytych punktów ekipy z San Antonio to: 80, 115, 108, 111, 83, 125, 109, 93, 95, 106. Średnia wyciągnięta z tego szeregu to 102,5 punktu, natomiast mediana wskazuje na to, że średnią wartością liczby zdobywanych przez drużynę punktów jest 107 punktów na mecz.

Jak widać średnia arytmetyczna jest zaniżona przez skrajną wartość 80 punktów w meczu z Miami Heat.

Podobnie jest w wielu przypadkach, dlatego warto jest wykorzystywać te dwie miary i porównywać je ze sobą. Nie tylko dzięki temu będziemy lepiej poinformowani o pewnych trendach liczbowych, ale również nie będziemy tak często wpadać w pułapkę jaką zastawia na graczy średnia arytmetyczna.

Legalni bukmacherzy, Poradnik bukmacherski

Przeczytaj również:

  1. Strategia obstawiania faworytów w zakładach bukmacherskich
  2. Bonusy w zakładach bukmacherskich
  3. Kryterium Kelly’ego w zakładach bukmacherskich
  4. Colorado Rockies – Arizona Diamondbacks

Spodobał Ci się ten artykuł? Oceń go i zostaw komentarz lub ocenę ze swojej strony.

Dodaj komentarz:

słabejest okdobrebardzo dobrerewelacja (1 głosów, ocena: 5,00)
Loading...




Superbet
Ostatnie artykuły:
Najpopularniejsze artykuły: