W pierwszej części serii artykułów poświeconych zastosowaniu statystyki w zakładach bukmacherskich i hazardzie przedstawione zostały dwie miary tendencji centralnej: średnia arytmetyczna oraz mediana.

Wskaźniki te informują nas o przeciętnej wartości i środkowej wartości zbioru danych. Jednak miary tendencji centralnej nie oddają nam pełnego obrazu zbiorowości.

Średnia arytmetyczna i mediana to najpopularniejsze wartości statystyczne, jednak aby uzyskać więcej informacji o interesującym nas zbiorze danych potrzebujemy jeszcze paru wskaźników.

W tym artykule opisano czym jest rozstęp, rozstęp międzykwartylowy, wariancja i odchylenie standardowe oraz jak je wyliczać.

Nie chcę robić powtórki z rozrywki, dlatego pominę na wstępie definicje matematyczne i wyłożę temat od razu na konkretnym przykładzie. Załóżmy, że chcemy dokonać zakładu na to, który z zawodników przeciwnych drużyn koszykówki zdobędzie więcej punktów w meczu.

Do wyboru mamy zawodników: Toma i Manu. A oto ich wyniki z dziesięciu ostatnich spotkań (dla uproszczenie obliczeń zakłada się, że obaj gracze spędzili w każdym meczy tyle samo czasu na boisku):

Tom: 15, 26, 7, 31, 23, 10, 20, 15, 19, 17
Manu: 25, 18, 6, 23, 9, 9, 4, 21, 20, 28

Porządkujemy dane w kolejności od najmniejszej do największej i otrzymujemy takie oto szeregi liczb:

Tom: 7, 10, 15, 15, 17, 19, 20, 23, 26, 31
Manu: 4, 6, 9, 9, 18, 20, 21, 23, 25, 28

Ktoś mógłby już w tym momencie gołym okiem stwierdzić, który zawodników jest lepszy. Zapewne wcale by się nie mylił, jednak celem tego przykładu jest pokazanie krok po kroku analizy takich danych, bo nie zawsze widać na pierwszy rzut oka kto ma stabilniejszą i lepszą formę.

Średnia arytmetyczna i mediana

Na podstawie wzorów z poprzedniej części możemy wyliczyć średnią arytmetyczną i medianę punktów. Tom średnio zdobywa 18,3 punktów, a jego mediana wynosi 18. Natomiast Manu przeciętnie zdobywa 15,3 punktów, a jego mediana to 19.

Miary tendencji centralnej nie pokazują nam tego co dzieje się w środku szeregu, dają nam tylko pewien obraz jego przeciętności. Średnie ukazują nam reprezentatywne wartości zbioru jednak nie wiadomo jak bardzo te dane są rozproszone. Najszybciej i najprościej można uzyskać informację o rozproszeniu danych obliczając rozstęp.

Rozstęp

Rozstęp pozwala na zobrazowanie tego jak bardzo zmieniają się wartości cechy statystycznej, a oblicza się go w bardzo prosty sposób. Wystarczy od najwyższej wartości szeregu odjąć najmniejszą jego wartość. W ten sposób otrzymamy różnicę, która mówi nam o tym na jakiej szerokości rozproszone są nasze dane.

I tak rozstęp w przypadku wyników Toma wynosi: 31-7 = 24, a w przypadku Manu: 28-4 = 24.

Obie wartości są identyczne co sugeruje, że obaj zawodnicy mają podobne wahania formy. Jednak rozstęp obliczany w tej najprostszej formule, ma bardzo istotną wadę – podobnie jak średnia arytmetyczna jest on bardzo wrażliwy na obserwacje nietypowe, czyli skrajne.

Rozstęp międzywkartylowy

W naszym przykładzie nie ma takich nietypowych obserwacji, jednak zobaczmy co by było gdybyśmy na koniec szeregu punktów zdobytych przez Manu zamiast liczby 28 wstawili 40 punktów. Mediana pozostała by bez zmian, natomiast średnia arytmetyczna i rozstęp bardzo by wzrosły. Dlatego o wiele lepszą metodą na obliczanie szerokości rozproszenia danych jest wyliczanie rozstępu międzykwartylowego.

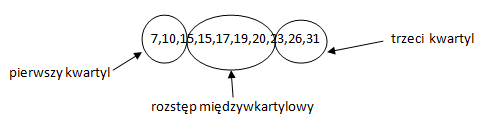
Na przedstawionym powyżej rysunku widoczny jest uporządkowany szereg punktów zdobytych przez Toma.

By policzyć kwartyle, należy podzielić zbiorowość na cztery równe części. Kwartyl pierwszy dzieli zbiorowość 25% i 75%, kwartyl drugi (mediana) na połowy, a kwartyl trzeci na 75% i 25%.

W naszym przykładzie, gdzie mamy zbiór dziesięciu liczb drugi kwartyl będzie znajdował się między drugą i trzecią pozycją w zbiorze, a trzeci pomiędzy ósmą i dziewiątą pozycją. Zatem, podobnie jak w przypadku wyliczaniu mediany w parzystym zbiorze danych, należy wyciągnąć średnią arytmetyczną z sąsiadujących ze sobą liczb.

Pierwszy kwartyl = Q1 = (10+15)/2 = 12,5
Drugi kwartyl = Q2 = (23+26)/2 = 24,5
Rozstęp międzywkartylowy = 24,5-12,5 = 12

Analogicznie postępując z danymi Manu wyliczymy, że rozstęp międzykwartylowy wyniesie 16,5 punktów.

Rozstęp liczony najprostszą metodą nie dał nam zbyt wiele informacji na temat tych zawodników, gdyż obaj uzyskali tą samą wartość 24 punktów. Dopiero rozstęp międzykwartylowy uzmysłowił nam jak bardzo różnią się wyniki obu zawodników, na dodatek jest on niewrażliwy na skrajne wartości szeregów, dzięki czemu jego wartość w rzetelniejszy sposób oddaje szerokość rozproszenia danych.

Tom uzyskał wynik o 4 punkty lepszy od Manu, co świadczy o tym, że jego wyniki są mniej rozproszone. Oczywiście rozstęp można również liczyć na inne sposoby.

Bonus powitalny w Forbet!

Typujesz piłę nożną i szukasz legalnego bukmachera? Sprawdź ofertę bukmachera Forbet. Odbierz 500 PLN bonusu na start, jest to 100% pierwszej wpłaty… [czytaj więcej o Forbet…]

Przy większej liczbie danych można zbiorowość podzielić na dziesięć części otrzymując tym samym decyle, lub na sto części otrzymując percentyle. Jednak w przypadku bukmacherki decyle i percentyle nie mają szczególnego zastosowania, ponieważ są za bardzo rozciągnięte w czasie.

Podsumowując to co obliczyliśmy do tej pory wychodzi na to, że znamy reprezentatywną wartość zbioru (średnia arytmetyczna i mediana) oraz rozproszenie zbioru (rozstęp i rozstęp międzykwartylowy).

Jednak aby lepiej zinterpretować nasze dane potrzebowalibyśmy jeszcze czegoś co pozwoli nam ocenić jak średnio zróżnicowane są wyniki od średniej arytmetycznej zbioru. Jednym słowem potrzebna nam miara rozrzutu, a taką właśnie jest wariancja.

Wariancja

Wariancję wyznacza się jako średnią kwadratów odchyleń poszczególnych wartości od ich wartości średniej arytmetycznej.

Można tą takiego oto wzoru:

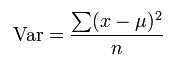
Gdzie:
x- wartość ze zbioru
µ- średnia arytmetyczna
n- ilość obserwacji w zbiorze

Powyższy wzór jest dosyć niewygodny dla tych, którzy liczą „na piechotę” dlatego zamiennie można używać tego wzoru:

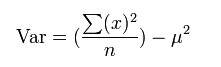
W zasadzie nawiasy w tym wzorze są zbędne, gdyż w pierwszej kolejności i tak wykonujemy potęgowanie i dzielenie a dopiero na końcu odejmowanie.

Obliczmy zatem wariancję dla wyników Toma.

Wariancja = (49+100+225+225+289+361+400+529+676+961/10)-334,89=(3815/10)-334,89=46,61

Podobne obliczenia wykonujemy dla Manu i otrzymujemy wynik 96,61

Otrzymane liczby niestety o niczym konkretnym jeszcze nas nie informują. Dlatego więc żeby uzyskać jakąś konkretną informację, trzeba obliczyć odchylenie standardowe (σ- symbol sigma).

Odchylenie standardowe

Odchylenie standardowe jest pierwiastkiem kwadratowym wyciągniętym z wartości wariancji i mówi nam o mierze odległości danych od ich średniej.

Zapis matematyczny wygląda tak:
σ = (wariancja)^1/2
lub
σ^2 = wariancja

Tak więc:
σ Toma = (46,61)^1/2 = 6,8 punktów
σ Manu = (96,61)^1,2 = 9,87 punktów

Wniosek jest prosty, wyniki Toma są bardziej skupione wokół średniej, świadczy o tym mniejsza wartość odchylenia standardowego. Mówi ona nam o tym, że przeciętnie wyniki Toma wahają się w granicach +/- 6,8 punktów od średniej arytmetycznej. Im mniejsza wartość σ tym lepiej jeśli chcemy aby dane były skupione wokół średniej arytmetycznej badanego zbioru.

Wnioski

Mając już najważniejsze wyliczenia dla wyników Toma i Manu można stwierdzić, że mając te same kursy na obu zawodników lepiej postawić na Toma. Ma on wyższą średnią zdobywanych punktów, na dodatek jego forma jest stabilniejsza, o czym świadczy niższa wartość odchylenia standardowego oraz mniejszy niż u Manu rozstęp międzywkartylowy.

Dla podanych w tym przykładzie danych można jeszcze wyliczyć kilka wskaźników, jednak te które zostały przedstawione w dwóch pierwszych częściach artykułów z tej serii są najczęściej używane i najbardziej praktyczne.

Mam nadzieję, że za pomocą powyższych przykładów w sposób jasny i klarowny objaśniłem zastosowanie i sposób obliczania tych jakże ważnych i potrzebnych dla profesjonalnych hazardzistów wskaźników.

Legalni bukmacherzy, Poradnik bukmacherski

statystyki bukmacherskie

Spodobał Ci się ten artykuł? Oceń go i zostaw komentarz lub ocenę ze swojej strony.

Dodaj komentarz:

5 komentarzy wpisu "Zastosowanie statystyki w zakładach bukmacherskich cz. 2"

Lukasz, wtorek, 28 sty 2014 21:13 



Chciałbym uświadomić twórcę artykułu Zastosowanie statystyki w zakładach bukmacherskich cz. 2 o tym że średnia arytmetyczna dla zawodnika Manu została źle obliczona, powinna wynosić 16,3 a nie jak w artykule 15,3. Co za tym idzie Wariancja i odchylenie standardowe tez są źle przedstawione. Wariancja dla Manu to nie 96,61 a 66,01 no i odchylenie nie 9,87 a 8,12.

pawel, środa, 28 cze 2017 11:54 



GIT dobry przykład – nie gram ale potrzebowałem czegos sensownego dla celu zrozumienia pojec statystycznych – dla mnie genialny przykład powiazany z praktykcznym zastosowaniem :-))…. i ta sigma – super pozdrawiam

tomaszek, sobota, 21 wrz 2019 16:15 



Otoz to panie Pawle.
Ja rowniesz poczulem energie tworcy artykulu od samego poczatku.
Nalezy tutaj uwzglednic CHEC DZIELENIA SIE POSIADANA WIEDZA – nie kazdy jest tak szczodrobliwy.

W takim celu jest obmyslana matematyka!
Zycie to walka, a matematyka rozwijana przez slabiej obdazonych matura. Urabiaja silnych fizycznie inaczej 😉 hehe

tomaszek, sobota, 21 wrz 2019 16:20 



Osobiscie jestem przeciwnikiem wykorzystywania tej wiedzy w takim celu a tez i hazard/bukmacherke uwazam za niegodziwe.

Tesla dla przykladu palal żądza ujarzmiania sil natury.
Plugawstwo z kolei podlapalo patenty ujarzmiajac kopaczy wegla.
Jestem przeciwny takim zastosowaniom tej wiedzy!

Art, środa, 17 lis 2021 4:34 



Witam,czy powyższe obliczenia można stosować także dla zespołów? Czy tylko jednostek. Pozdrawiam

Warning: Undefined variable $user_ID in /home/www/darmowa-kasa.pl/p/wp-content/themes/wpsn/comments.php on line 76

(Oceń ten artykuł!)

Loading...

Imię

Adres e-mail

Strona www

Δ

Ostatnie artykuły:

• Zakłady blokowe i rozpisowe. Co to?
• Darmowe bonusy na tenis ziemny od bukmachera Superbet
• Bukmacher Betfan płaci za gole Lewego!
• CR7 w Manchesterze City? Sprawdź kursy bukmachera Betfan!
• Zakłady przedmeczowe i na żywo na tym samym kuponie u bukmachera forBET

Najpopularniejsze artykuły:

• Surebets – czyli pewny zysk!
• Jak dobrze obstawiać Zakłady Na Żywo? Typowanie LIVE
• Płatne typy – hit czy kit?
• Jak skutecznie obstawiać ligę baseball’u MLB?
• Jak przechytrzyć bukmachera? Eksperci radzą!
• Bukmacher Superbet
• Zakłady blokowe i rozpisowe. Co to?
• 7 przykazań skutecznego typera!
• Poradnik typera zakładów bukmacherskich
• Zakłady blokowe i rozpisowe